In diesem Anwendungsfall führen wir eine FEM-Analyse mit Parameteridentifikation und Schaltungssimulation eines Universalmotors durch. Es werden die typischen Kenngrößen Drehzahl und Strom über Drehmoment ermittelt.
Ausgangs-Situation
Typische Merkmale ermitteln
In dieser Anwendung wird gezeigt, wie die typischen Eigenschaften eines Universal- oder Reihenschlussmotors bestimmt werden können. Diese Motoren, die in einem Bereich von weniger als 1000 Watt arbeiten, werden in vielen Haushaltsgeräten wie Bohrmaschinen, Staubsaugern und Mixern eingesetzt.
Bild: Universalmotor eines Staubsaugers (Wikipedia)
Die Maschine wird als Reihenmotor bezeichnet, weil die Erregerwicklung mit der Rotorwicklung in Reihe geschaltet ist. Außerdem wird er als Universalmotor bezeichnet, weil er sowohl mit Wechsel- als auch mit Gleichstrom betrieben werden kann.
Die Drehzahl eines Universalmotors kann sehr hoch sein, typischerweise im Bereich von 5000-30000 U/min. Die Drehzahl ist völlig abhängig von der Last und der Versorgungsspannung. Ohne Last kann ein Universalmotor gefährlich hohe Drehzahlen erreichen. Tatsächlich wird die Leerlaufdrehzahl nur durch Reibungs- und Windungsverluste begrenzt.
Angegeben sind technische Zeichnungen für den Abschnitt sowie das Wicklungsschema in einem typischen Format.
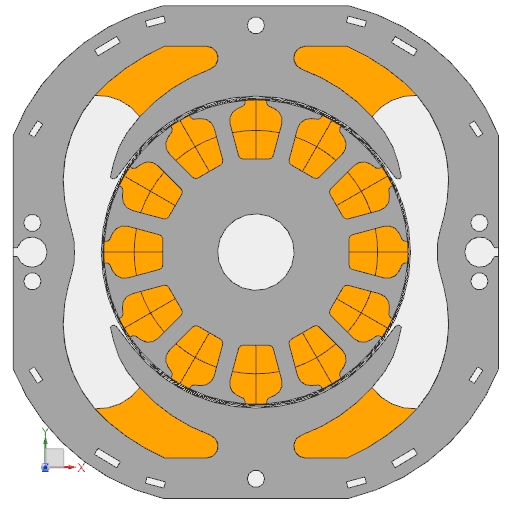
Abbildung: CAD-Modell eines Ausschnitts des untersuchten Universalmotors
Die hier vorgestellten Methoden basieren auf der folgenden Literatur: H. Grop "Modeling of a universal motor with speed control", Royal Institute of Technology Department of Electrical Engineering Electrical Machines and Power Electronics, Stockholm 2006.
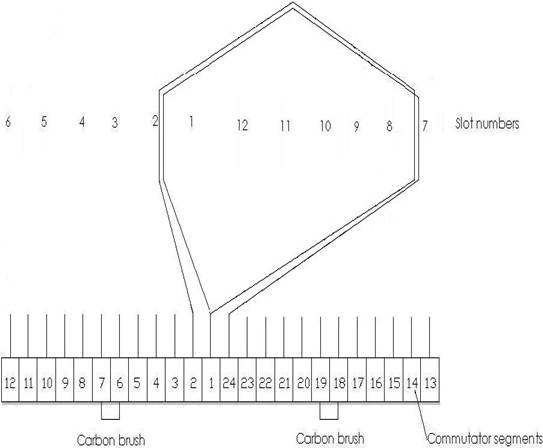
Bild: Windungs-Schema
Geeignete Methode
Äquivalenzschaltungen und Systemgleichungen
Nach der Literatur wird das folgende Ersatzschaltbild mit den zugehörigen Systemgleichungen für den Universalmotor verwendet.
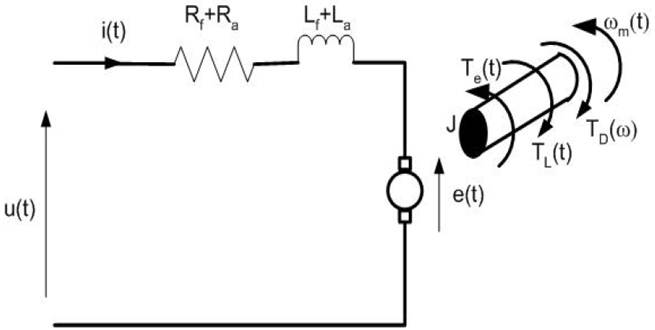
Bild: Äquivalenzschaltung für Universalmotor
Ra, Rf: Rotor- und Feldwicklungswiderstand,
La, Lf: Läufer- und Feldwicklungsinduktivität,
u(t): Klemmenspannung,
e(t): Gegen-EMK,
i(t): Strom in der Maschine,
D: viskose Dämpfungskonstante,
J: Trägheitsmoment von Maschine und Last,
T(t), Tl: elektromagnetisches und Lastmoment,
ωm(t): Winkelgeschwindigkeit der Maschine,
Ka: Rotorkonstante (bekannte Parameter),
Kψ: Flusskonstante.
Parameteridentifikation
Unbekannte oder nichtlineare Parameter, die von der magnetischen Sättigung abhängen, sind die Induktivität der Feldwicklung Lf und die Flusskonstante Kψ. Diese Parameter werden mit Hilfe von Magnetics for NX bestimmt.
Dazu wird ein nichtlineares FEM-Modell der Maschine in NX mit dem Magnetics-Solver erstellt. Die nichtlinearen BH-Kurven der Materialelektrobleche wurden dem Verteiler entnommen.
Wir legen Stromstärken von 0,1 bis 20 Ampere an die Spulen an, um die Felder zu berechnen und die Auswirkungen der nichtlinearen Sättigung zu berücksichtigen. Aus den Ergebnissen leiten wir die Werte Lf und den magnetischen Fluss, der durch einen Pol fließt, als Funktion des Stroms ab, wie Sie in den beiden Bildern sehen können.
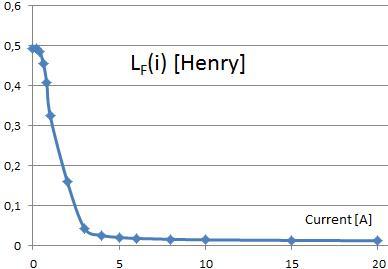Bild: Induktivität als Funktion des Stroms ermittelt
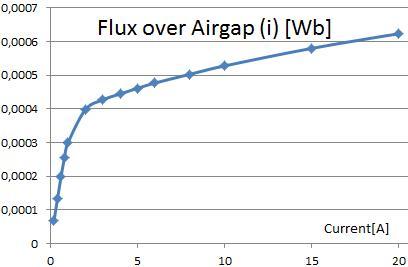Bild: Fluss über Luftspalt, ermittelt durch FEM-Analyse
Aus der Schaltung und den Gleichungen können wir nun ein Systemsimulationsmodell ableiten. Dieses Modell wird mit den von der FEM berechneten Werten Lf(i) und Flux(i) gespeist. Diese sind als Nachschlagetabellen enthalten.
Ergebnisse
Geschwindigkeit und Strom über Drehmoment
Das Systemmodell kann gelöst werden, um viele verschiedene Ergebnisse zu erhalten. Die nächsten beiden Bilder zeigen das Verhalten von Drehzahl und Strom über dem Drehmoment.
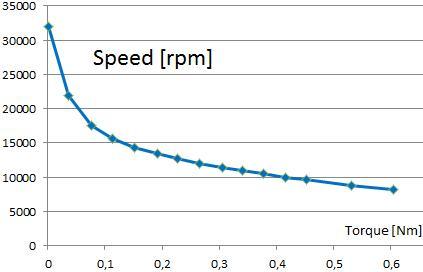Bild: Geschwindigkeit über Drehmoment Ergebnis
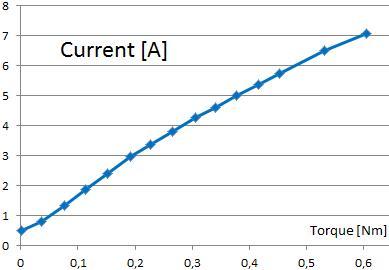
Bild: Strom über Drehmoment Ergebnis
Flußdichte und Potentiallinien
Ein weiteres interessantes Ergebnis der FEM-Analyse ist die Flussdichte. Diese Darstellung gibt nützliche Informationen über die Nutzung von Geometrie und Material.
Bild: Flussdichte im Contourplot
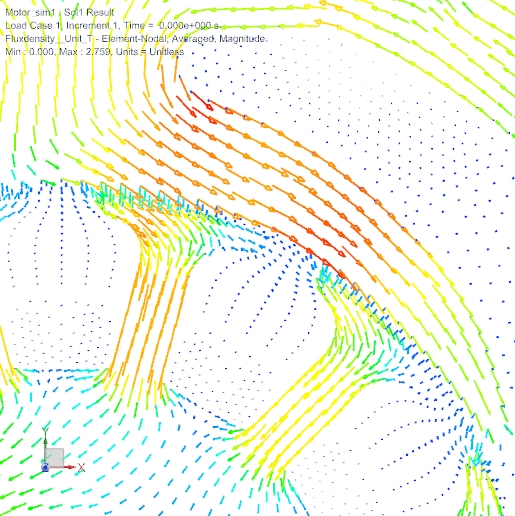
Bild: Flussdichte als Vektordiagramm
Auch Potenziallinien können nützliche Informationen liefern. Das folgende Bild zeigt die Richtung des Drehmoments und der Rotation: Dieser Motor wird gegen den Uhrzeigersinn laufen.
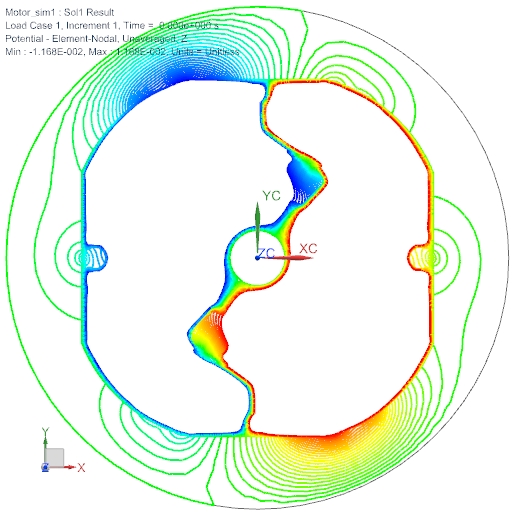
Bild: Potentiallinien zeigen Richtung des Drehmoments
