Motor Analyse für NVH

Dieses Beispiel zeigt, wie ein Servomotor mit MAGNETICS und NX NASTRAN analysiert wird. Die magnetischen Kräfte an 36 Zähnen werden auf eine strukturelle (akustische) Lösung übertragen,

Download as PDF     Download NX Files

die Antworten auf die vorherrschende Lärmfrequenz und den Druck gibt.

Ausgangs-Situation

Statorschwingungen erzeugen Lärm

Vibrationen und Geräusche von Elektromotoren in Läufern entstehen hauptsächlich durch die Verformung des Stators, die durch das sich ständig ändernde Magnetfeld verursacht wird, das die einzelnen Phasen aktiviert. Die Verformung an der Außenfläche des Motors bewirkt, dass sich die Luft um ihn herum bewegt, wodurch Druckunterschiede entstehen, die vom menschlichen Ohr als Lärm wahrgenommen werden. Bei dieser Analyse sind drei Disziplinen zu berücksichtigen - die magnetische, die schwingungstechnische (strukturelle) und die akustische [SantosAnthonisNaclerioGyselinck].

In diesem Anwendungsbeispiel analysieren wir einen Servomotor für die magnetischen und schwingungstechnischen (strukturellen) Disziplinen mit MAGNETICS für NX und NX NASTRAN. Für den dritten Teil, die Akustik, kann auch NX NASTRAN verwendet werden, aber wir werden es hier nicht zeigen, da wir uns auf den magnetischen Teil konzentrieren.

Ziel ist es, herauszufinden, welche Frequenzen auftreten und welche hauptsächlich Geräusche erzeugen, während der Motor mit der gegebenen Geschwindigkeit läuft.

Referenzen:

“Multiphysics NVH Modeling: Simulation of a Switched Reluctance Motor for an Electric Vehicle”, Fábio L. M. dos Santos, Jan Anthonis, Francesco Naclerio, Johan J. C. Gyselinck, Member, IEEE, Herman Van der Auweraer, Member, IEEE, and Luiz C. S. Góes. IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, VOL. 61, NO. 1, JANUARY 2014.

Geeignete Method2

2D Magnetisch, 3D Struktureller Ansatz

Die Ergebnisse basieren auf den magnetischen Kräften an den Zähnen. Dazu führen wir zunächst eine instationäre Analyse in 2D durch und berechnen die Kräfte an den Zähnen. Wir werden ein Postprocessing-Solver-Feature verwenden, das die zeitabhängigen Kräfte mittels Fourier-Transformation in frequenzabhängige Kräfte umwandelt. Dann werden diese frequenzabhängigen Kräfte in NX10 importiert, wobei das in NX10 neue Feature Lastrezept verwendet wird. Schließlich wird in NX eine Frequenzganganalyse in NX NASTRAN Solution 111 mit diesen Kräften als Eingabe durchgeführt.

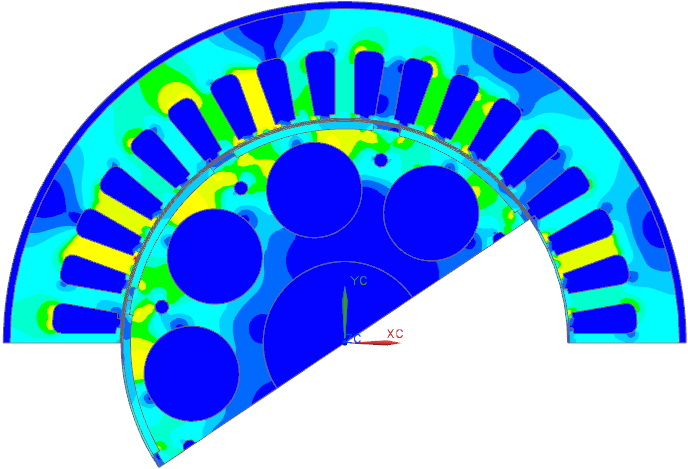
Abbildung: Vollständiges Simulationsmodell eines 1FT6-Motors. Flussdichteverteilung im 1FT6 Servomotor. Zwei der vier Pole sind mit Periodizitätsbedingungen modelliert. Klicken Sie zum Animieren

Ausgangspunkt ist ein bereits vollständiges Simulationsmodell eines Servomotors. Wir überprüfen es zunächst und fügen dann die notwendigen Schritte für den NVH-Export hinzu und lösen es in NX NASTRAN. Das Modell muss wie in der folgenden Abbildung dargestellt vorbereitet werden: Im Luftspalt unter jedem Zahn muss eine separat vernetzte Fläche definiert werden.

 

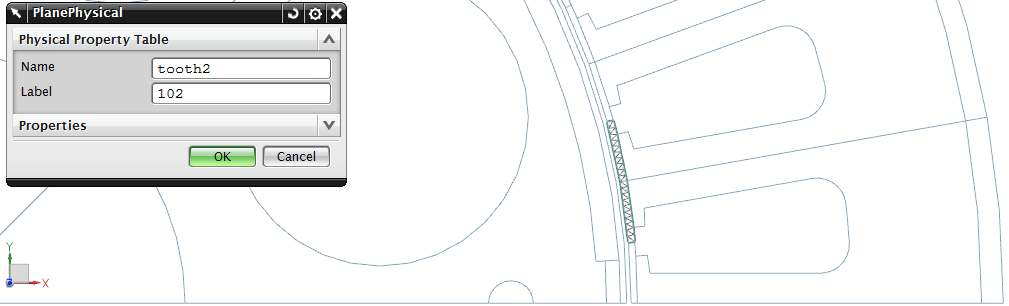Bild: Gesichter im Luftspalt, auf denen die Kräfte berechnet werden

 

Tangentiale und radiale Kräfte werden mit den folgenden Gleichungen berechnet, die auf dem Maxwell-Spannungstensor basieren, der auf den zuvor definierten Zahnflächen ausgewertet wird.

Die Kräfte sollten im ersten Schritt überprüft werden. Sie erscheinen wie im oberen Teil des folgenden Bildes, das die Kräfte für den ersten Zahn zeigt.

 

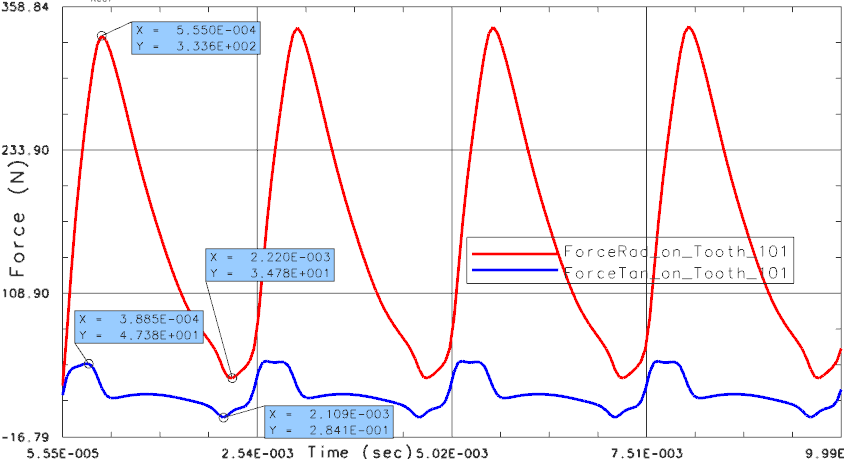
Abbildung: Das Simulationsmodell berechnet im Zeitbereich die Kräfte auf die 36 Zähne in radialer und tangentialer Richtung

 

Nun werden die Kräfte im Zeitbereich in den Frequenzbereich Fouriertransformiert. So erhalten wir für jeden Zahn Real- und Imaginärteil als Funktion der Frequenz. Dies wird im nächsten Bild gezeigt.

 

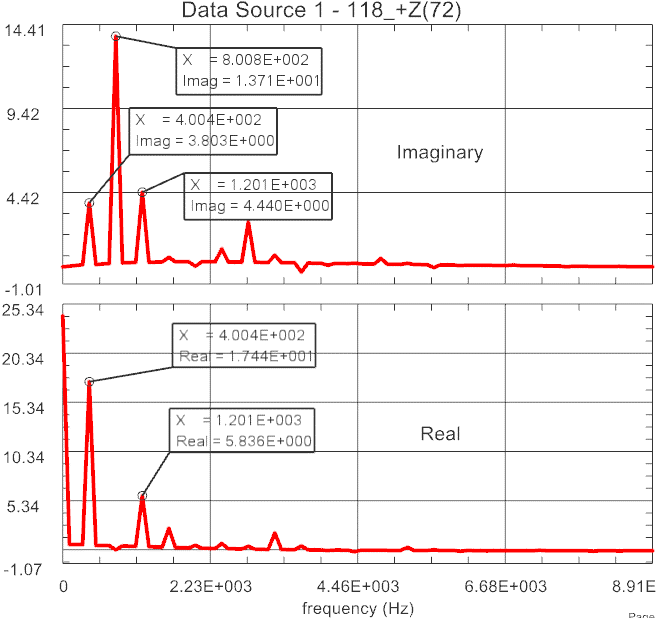
Bild: Fourier transformierte Kräfte

 

 

 

 

Ergebnisse

Frequenz für höchsten Schalldruck

Im nächsten Schritt wird in NX ein 3D-Modell für die FE-Strukturanalyse erstellt, was einfach durch Extrudieren der Statorflächen erfolgen kann. Um effizient zu arbeiten, sollte dies mit der Assembly-Fem-Methode erfolgen, die es ermöglicht, nur einen Zahn zu vernetzen und diesen 36 Mal wiederzuverwenden.

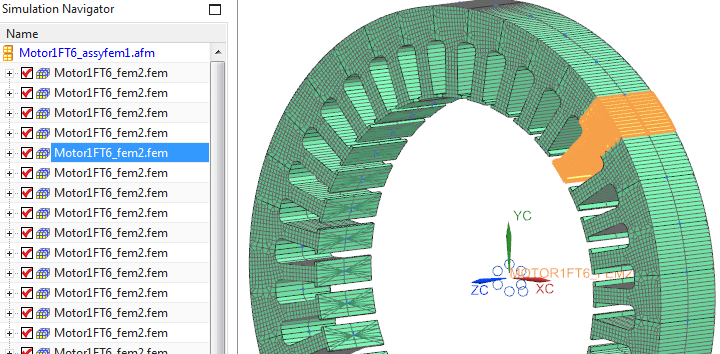Bild: 3D-Struktur-Assembly-mesh in NX für den Stator

Alle zuvor berechneten Frequenzbereichskräfte werden nun mit der NX-Funktion "Lastrezept" auf das Strukturnetz angewendet. Die Zuordnung zu den 36 Zähnen muss nur beim ersten Mal manuell vorgenommen werden. Bei Änderungen im Magnet- oder Strukturmodell ist eine vollautomatische Aktualisierung möglich.

Das FE-Strukturmodell kann nun zur Durchführung von NX NASTRAN-Simulationen des dynamischen Verhaltens verwendet werden (Lösung 111). Zur Validierung der berechneten Ergebnisse zeigen wir eine Tabelle mit Frequenzen und den entsprechenden maximalen Amplituden. Diese Informationen werden aus den Ergebnissen extrahiert.

Frequenz [Hz]                  max. Amplitude [mm]
100.1                                  0.000131
200.2                                  0.000116
300.3                                  0.000103
400.4                                  0.0029
500.5                                  0.000067
600.6                                  0.000068
700.7                                  0.000072
800.8                                  0.002167
900.9                                  0.000109
1001                                   0.000178
...

Es ist zu erkennen, dass es bei 400,4 und 800,8 Hz Maxima in der Amplitude gibt, wie es in der Aufgabe gefordert wurde. Daraus ergibt sich der höchste Schalldruck bei dieser Frequenz. Schließlich zeigen wir die Verformungsform und die Spannungsverteilung (zum Animieren anklicken) für die Frequenz 400,4 Hz.

 

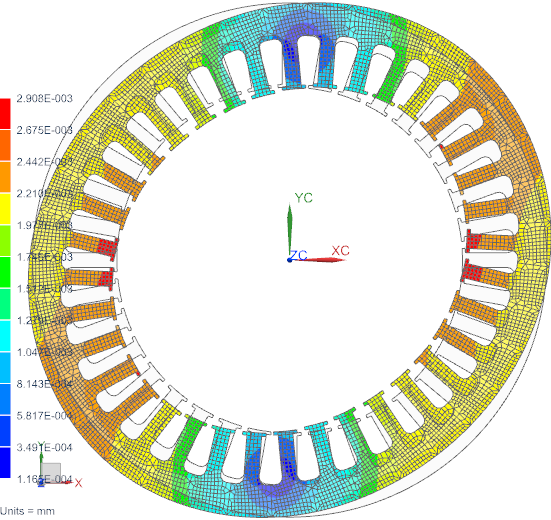
Abbildung: Verformungsform bei der kritischen Frequenz 400 Hz. Die Skala ist auf 100 eingestellt. Zum Animieren anklicken.

 

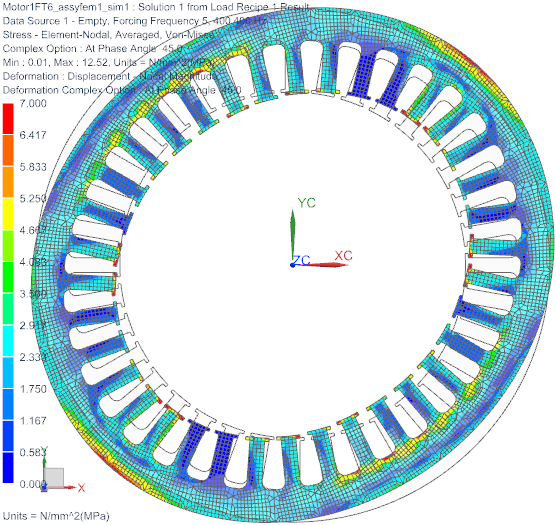
Abbildung: Von-Mises-Spannung bei kritischer Frequenz 400 Hz. Zum Animieren anklicken