Das Beispiel zeigt, wie die Leistung einer Test-Induktionsmaschine (asynchron) ermittelt und optimiert werden kann.
Von besonderem Interesse ist die Methode, die zur Parameteridentifikation verwendet wird: Induktivität und Ohmsche Widerstände werden mit FE berechnet. Mit diesen Werten wird eine analytische Netzaussage gespeist.
Ausgangs-Situation
Induktions-Maschiene
Wir wollen mit dem Programm Magnetics die Leistung einer Versuchsinduktionsmaschine bei Drehzahl und unter Last ermitteln. Dazu wollen wir die folgenden Kennlinien des Motors ermitteln:
- Drehmoment über Drehzahl,
- Wirkungsgrad über Drehzahl,
- Strom über Drehzahl.
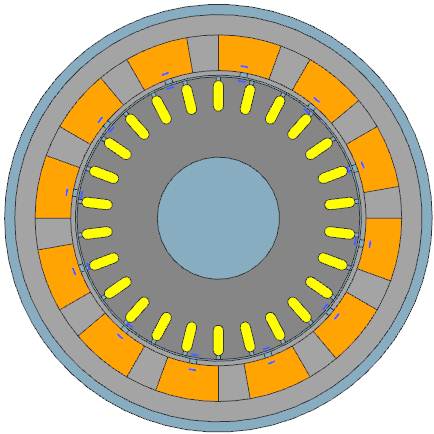Bild: CAD Modell des Motors
Einige der Merkmale dieses Motors sind:
- Anzahl der Nuten im Stator: 12
- Außendurchmesser des Stators: 400 mm
- Anzahl der Leiter des Rotors: 26
- Dicke: 162 mm
- Anzahl der Pole: 2
Die hier gezeigten Methoden basieren auf den folgenden Literaturen:
- Calculation of two-axis Induction Motor Model Parameters using Finite Elements
- und David Meeker's "Induction Motor Example".
Geeignet Methode
Kombiniert analytisch / FEM
Anstatt das Verhalten der Maschine direkt zu modellieren (dies könnte durch eine instationäre Analyse geschehen), werden wir die Leistung bei Geschwindigkeit und Last durch eine Reihe von Simulationen statischer Konfigurationen ableiten. Aus diesen Simulationen werden wir die Ersatzschaltkreisparameter der Maschine ableiten, die wir dann in einem analytischen elektrischen Schaltkreismodell verwenden werden. Der Vorteil eines analytischen Schaltkreismodells besteht darin, dass es eine sehr schnelle Analyse der verschiedenen Parameter ermöglicht.
Ein einphasiges Schaltungsmodell für einen Asynchronmotor ist in der folgenden Abbildung dargestellt.
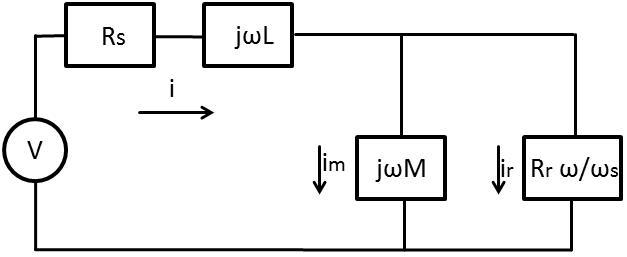Bild: Steady State Induktions Motor Modell
L: Induktivität der gesamten Streuung auf der Statorseite
M: Induktivität des magnetischen Kreises, der den Rotor und den Stator verbindet
Rr: Ohmscher Widerstand des Rotors
Rs: Ohmscher Widerstand des Stators
V: Phasenspannung, Effektivwert der Spannung an jeder Phase
i: Phasenstrom, Effektivstrom durch jede Phase der Maschine
ω: Elektrische Frequenz
ωs: Differenz zwischen der mechanischen Frequenz des Rotors und seiner elektrischen Frequenz.
Mit Hilfe der Finite-Elemente-Analyse ist es möglich, die Spuleninduktivitäten mit hoher Genauigkeit zu berechnen. Dies ist sehr hilfreich, da sie in analytischen Formeln zur Beschreibung der Schaltung verwendet werden können. In unserem Fall leiten wir die benötigten Induktivitätswerte auf folgende Weise ab: Wir führen eine Frequenzsweep-Analyse über 12 niedrige Frequenzen durch.
Als Ergebnis erhalten wir Real- und Imaginärteile für 12 Induktivitäten. Wir lassen diese Werte durch einen implementierten Parameter-Fitting-Algorithmus laufen und erhalten als Ergebnis die angepassten Werte für L1, M, Rr :
L = 34,6 mH Stator-Streuinduktivität
M = 139,5 mH Gegeninduktivität zwischen Rotor und Stator
Rr = 0,31 Ohm Rotorwiderstand bei Raumtemperatur
Als nächstes passen wir die Werte für den Rotorwiderstand an die Temperaturerhöhung von 60°C an und berechnen auch den Statorwiderstand auf Rr = 1 Ohm
Ergebnisse
Drehmoment, Effizienz, Strom
Alle diese Daten, die sich aus der FE und Analytik ergeben, speichern wir in einem übersichtlichen Mathcad-Dokument. Dies ermöglicht dem Benutzer auf bequeme Weise, die verwendeten Formeln zu verstehen und zu manipulieren.
In dem Dokument werden die Formeln ausgewertet, die sich aus dem Schaltungsmodell ergeben. Das Ergebnis sind die charakteristischen Graphen, die den Motor beschreiben. Nun kann der Motor ausgewertet werden.
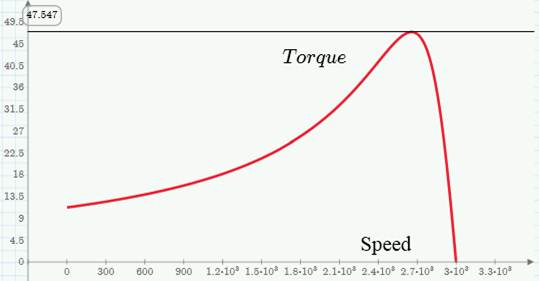Bild: Die Drehmomentkurve zeigt das charakteristische Verhalten eines Asynchronmotors
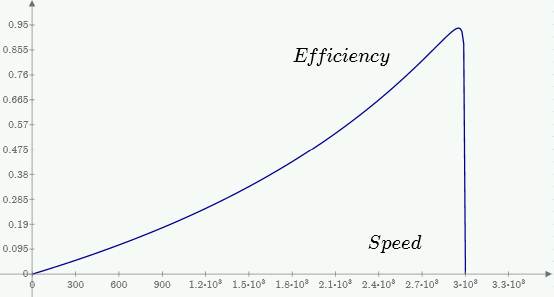
Bild: Die Kurve der Effizienz
Bild: Der Strom des Motors
Ein weiterer Vorteil ist die automatische Aktualisierung des Diagramms, wenn Sie die Eingangsparameter ändern. Wenn also die Motorparameter geändert werden, kann sofort erkannt werden, welche Auswirkungen dies auf die Grafik hat. Auf diese Weise ist es einfach, den Motor passend einzustellen und an die Anforderungen anzupassen.
