Die Feld- und Wirbelverluste im Kern, der aus laminierten Elektroblechen besteht, sind zu berechnen.
Download as PDF Download NX Files
Ausgangs-Situation
Demonstrations Transformator
Das Problem ist ein einfacher einphasiger Transformator, wie in der nächsten Abbildung gezeigt. Ziel ist es, an die Primärspule einen Wechselstrom und an die zweite Spule einen Widerstand als Lastbedingung anzulegen. Die Feld- und Wirbelverluste im Kern sollen berechnet werden. Der Kern ist aus laminierten Elektroblechen gefertigt. Die Ergebnisse sollen für verschiedene Blechdicken durchgeführt werden: Wir wollen einen Sweep von 0,1 bis 1 mm Dicke verwenden.
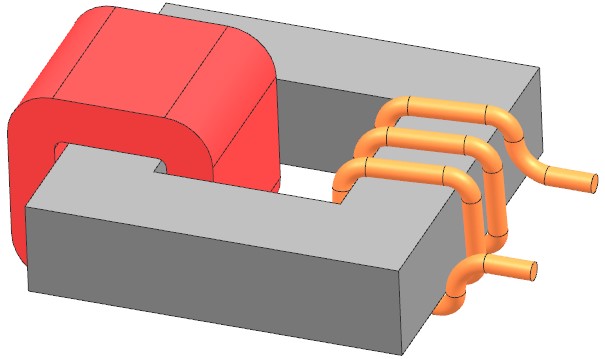 Bild: CAD-Modell des zu analysierenden Transformators
Bild: CAD-Modell des zu analysierenden Transformators
 Bild: FEM-Modell des Transformators
Bild: FEM-Modell des Transformators
Die meisten Elemente sind 3D-Hexaeder. Die Last auf der Sekundärspule wird durch einen 1D-Schaltkreis modelliert.
Einige vorgegebene Abmessungen sind diese:
- Länge des Transformators: 40 mm,
- Anzahl der Windungen der Primärspule: 237
- Füllfaktor der Primärspule: 0,6
- Anzahl der Wicklungen der Sekundärspule: 3
Geeignete Methode
3D Magnetodynamik Frequenzbereich mit Circuits
Diese Art von Problem wird in NX Magnetics mit Hilfe eines 3D-Magnetodynamik-Frequenzbereich-Lösungs-Typs und zusätzlich mit einem Schaltungsnetz für die Last auf der Sekundärspule gelöst. Natürlich gibt es auch andere Möglichkeiten. Alternative Ansätze wären Berechnungen im Zeitbereich, die es erlauben würden, nichtlineare Materialbedingungen zu berücksichtigen. Auch eine 2D-Analyse wäre sinnvoll. Die nächsten Bilder zeigen das Netz und einige Details dazu.
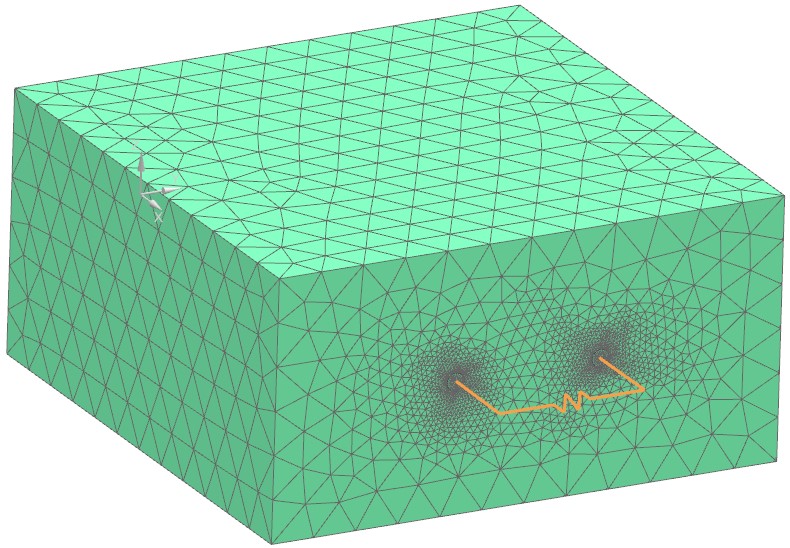 Bild: Um den Transformator herum befindet sich eine Air Box, in der das elektromagnetische Feld berechnet wird
Bild: Um den Transformator herum befindet sich eine Air Box, in der das elektromagnetische Feld berechnet wird
Als Nächstes wird die Vernetzung vorgenommen. Wir verwenden hexaedrische Elemente sowohl für die Spulen als auch für die Platten. Diese Elemente führen zu den besten Ergebnissen bei Finite-Elemente-Lösungen. Diese Elemente können leicht mit der Außenluft verbunden werden, die mit Hilfe von Pyramiden im Übergangsbereich vernetzt wird.
 Abbildung: Detailaufnahme der Sekundärspule, die als massiver Leiter modelliert ist. Alle Wirbelströme, Skin-Depth- und Proximity-Effekte im 3D-Modell werden durch diese Vernetzungsmethode erfasst.
Abbildung: Detailaufnahme der Sekundärspule, die als massiver Leiter modelliert ist. Alle Wirbelströme, Skin-Depth- und Proximity-Effekte im 3D-Modell werden durch diese Vernetzungsmethode erfasst.
 Bild: Detailaufnahme der Primärspule.
Bild: Detailaufnahme der Primärspule.
Diese Spule wird durch einen gwickelten (stranded) Ansatz modelliert, was bedeutet, dass jedes Element einen Vektor hat (siehe nächstes Bild), um die Wicklungsrichtung zu definieren
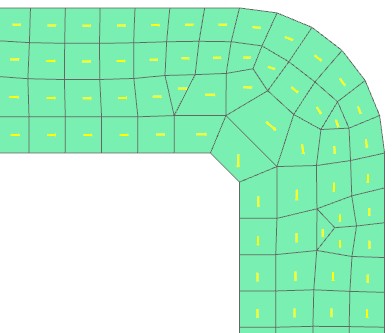 Bild: Definition der Förderrichtungen
Bild: Definition der Förderrichtungen
Um die Wirkung von Laminierblechen zu erfassen, verwenden wir eine Homogenisierungstechnik, die berücksichtigt, wie sich Wirbelströme im Falle dünner Bleche verhalten. Da die Wirbelströme das Feld beeinflussen, werden auch andere Ergebnisgrößen davon beeinflusst. In NX Magnetics wird diese Technik angewendet, indem ein Koordinatensystem für die Stapelrichtung zugewiesen wird, wie im nächsten Bild zu sehen ist.
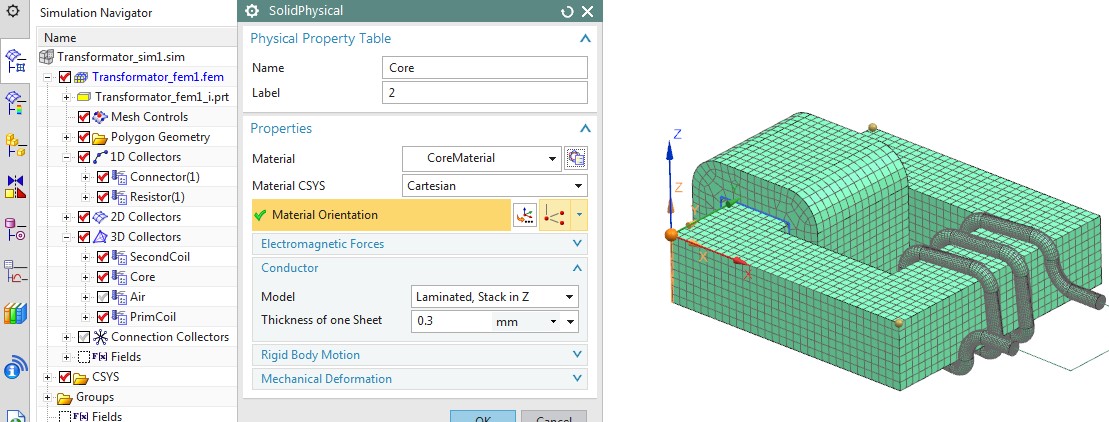 Bild: Die Anwendung der Laminationseffekte auf den Kern
Bild: Die Anwendung der Laminationseffekte auf den Kern
Wie in der Aufgabe beschrieben, werden wir Simulationen mit verschiedenen Dicken durchführen. Wir erwarten, dass die Verluste bei größeren Dicken zunehmen werden.
Der Stromkreis wird durch ein eindimensionales Element modelliert. Das Dialogfeld NX Magnetics sehen Sie in der nächsten Abbildung.
 Bild: Die Anwendung des Ohmschen Widerstandes auf das Schaltungselement
Bild: Die Anwendung des Ohmschen Widerstandes auf das Schaltungselement
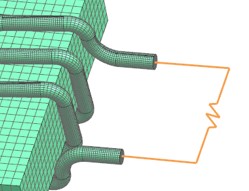 Bild: Das Schaltkreiselement.
Bild: Das Schaltkreiselement.
In der NX-Simulationsdatei richten wir eine magnetodynamische Lösung im Frequenzbereich bei 50 Hz ein. Wir nennen sie LaminationSweep, weil wir einen Parameter-Sweep über mehrere Blechdicken durchführen wollen. Das nächste Bild zeigt den Lösungsdialog und die gewünschten Ausgaben.
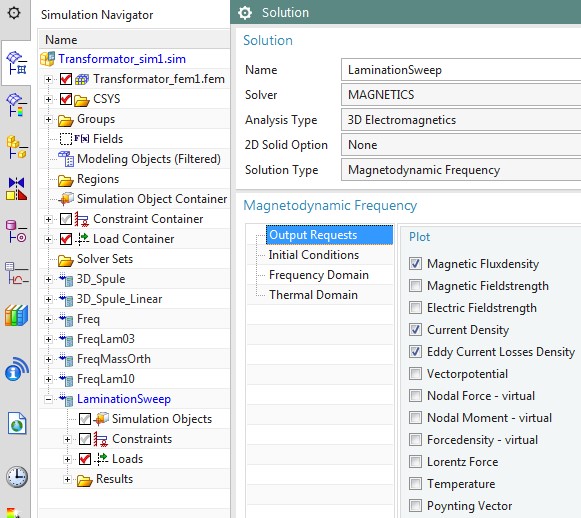
 Abbildung: Der NX Magnetics-Dialog für die Lösung und die Output Requests
Abbildung: Der NX Magnetics-Dialog für die Lösung und die Output Requests
Wir legen einen Spitzenstrom von 0,5 Ampere an. Dann richten wir den Parameter-Sweep ein. Wir variieren die Blechdicke, beginnend bei 0,1 mm und endend bei 1 mm mit einer Schrittweite von 0,1. Das Dialogfeld ParameterSweep ist in der nächsten Abbildung zu sehen.
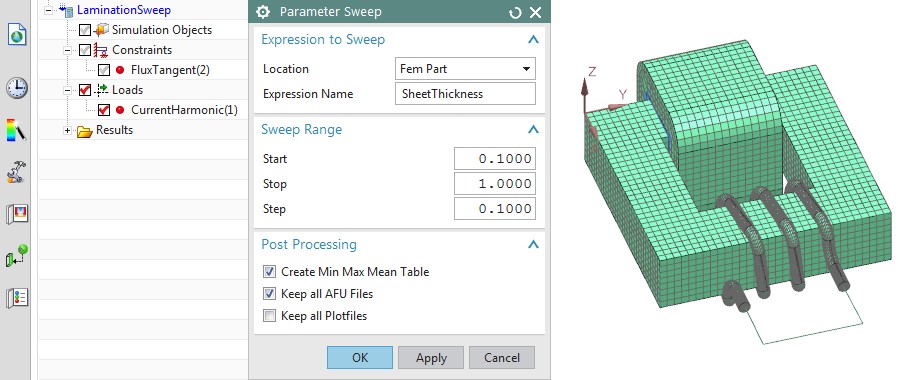 Abbildung: Der NX Magnetics-Dialog für den Parameter Sweep
Abbildung: Der NX Magnetics-Dialog für den Parameter Sweep
Die Lösungszeit hängt von dem verwendeten Computer ab. Sie kann zwischen 5 und 20 Minuten variieren.
Ergebnisse
Verlusttabelle, B Feld- und Wirbelströme
Nach einigen Minuten ist der Parameter-Sweep beendet und alle Ergebnisse können diskutiert werden. Wir beginnen mit den Wirbelstromverlusten auf dem Kern, die unser Hauptergebnis sind. Im Falle von Parameter-Sweeps wird dieses Ergebnis in Form einer Texttabelle ausgegeben, die z.B. in Excel angezeigt werden kann. Siehe nächstes Bild.
 Abbildung: Die berechneten Wirbelstromverluste im Kern in Abhängigkeit von der Laminatdicke
Abbildung: Die berechneten Wirbelstromverluste im Kern in Abhängigkeit von der Laminatdicke
Die Feldlösung ermöglicht einen detaillierten Einblick in das Verhalten der magnetischen, elektrischen und Wirbelstromfelder. Alle Ergebnisse können in realen, imaginären oder anderen Kombinationen aufgetragen werden. Solche Darstellungen helfen dem Benutzer zu verstehen, wie geometrische Details das Ergebnis beeinflussen. Das nächste Bild zeigt die magnetische Flussdichte.
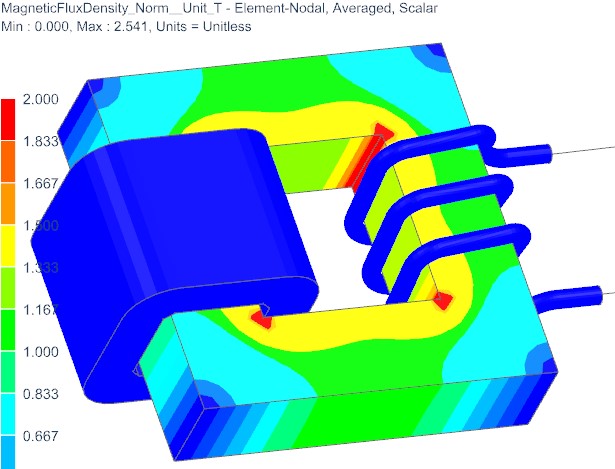 Bild: B-Feld am Transformator
Bild: B-Feld am Transformator
 Bild: B Feld (Vektor Ansicht) am Transformator
Bild: B Feld (Vektor Ansicht) am Transformator
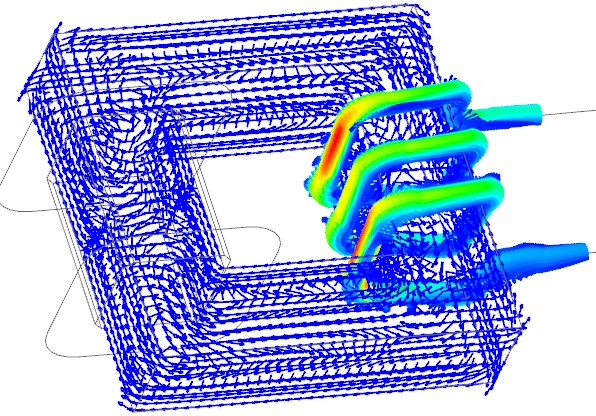 Bild: Wirbelstromfelder am Transformator
Bild: Wirbelstromfelder am Transformator
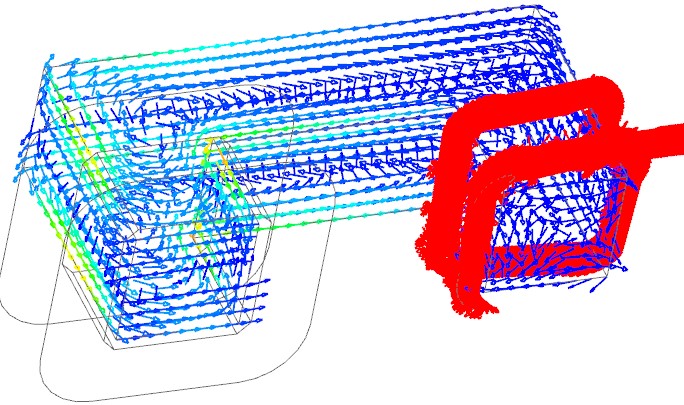 Bild: Wirbelströme am Transformator
Bild: Wirbelströme am Transformator
Leistung, Statistik:
- Gesamtzahl der Elemente: 225644
- Gesamtzahl der Knoten: 95955
- Anzahl der Hexa-Elemente: 62900
- Anzahl der Tetra-Elemente: 140987
- Lösungszeit pro Sweep-Schritt: 2 min
- CPU: 205 s.
- Verwendeter Speicher: 930 Mb
- Rechner: Intel Pentium i7, 4 Kerne



