In diesem Beispiel modellieren wir magnetische Hystereseeffekte mit Hilfe des Jiles-Atherton-Vektor-Hysteresemodells.
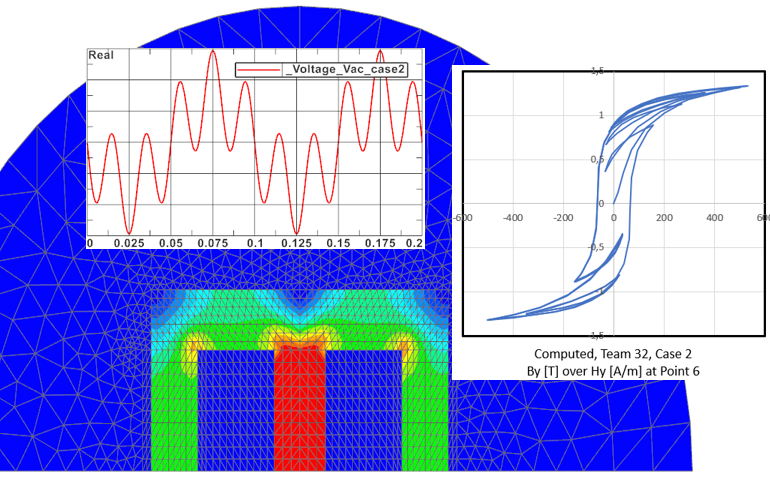
Ausgangs-Situation
Hysterese Modellierung
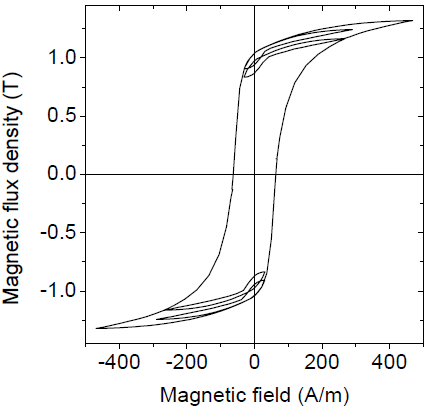
Das verwendete Beispiel ist der Testfall TEAM 32, dessen Aufbau in der folgenden Abbildung dargestellt ist. Das folgende Bild zeigt die erwartete Hystereseschleife, wie sie sich aus den magnetischen Wechselfeldern am Punkt C6 ergibt.
Abbildung: TEAM 32 Testfall und erwartete Hystereseschleife
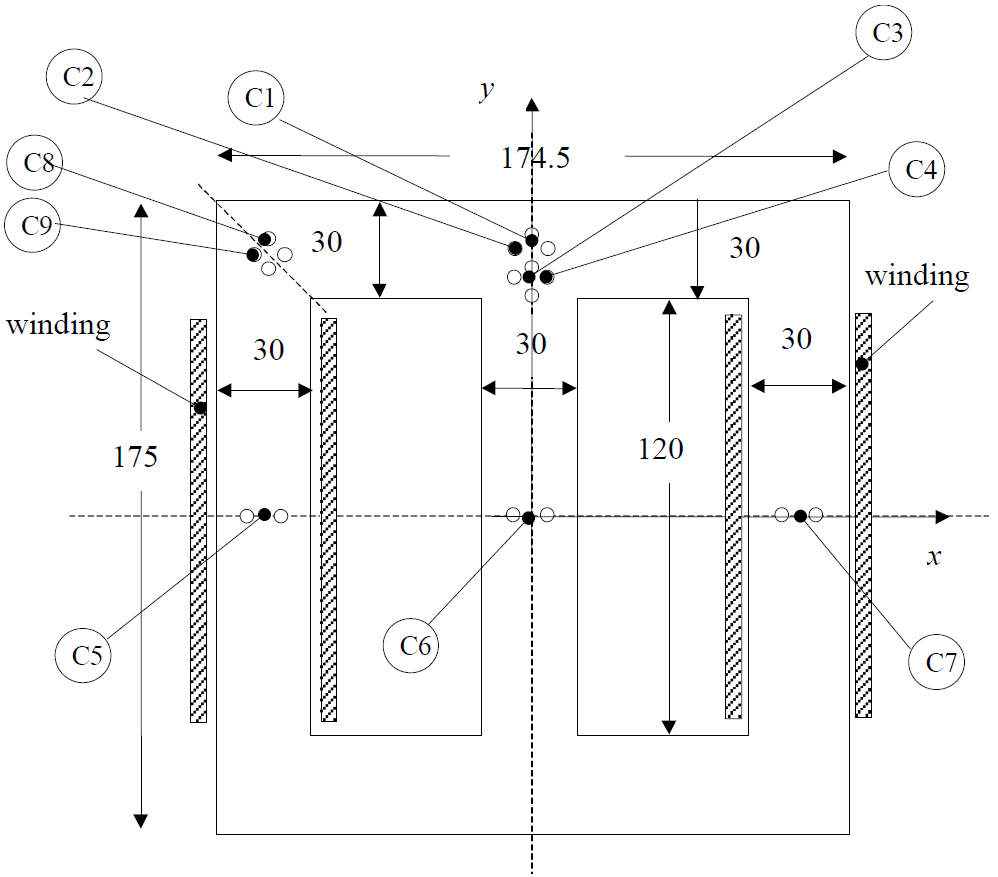
Die Abmessungen und Materialdaten sind dem TEAM-Benchmark-Problem 32 entnommen. Einige der Eingabedaten sind:
Spulen: Kupfer, 90 Windungen, Elektrische Leitfähigkeit 58e6 S/m
Kern: Magnetisch, nichtlinear, mit Hystereseparametern.
Weitere Hintergrundinformationen zu diesem Testbeispiel und den verfügbaren Messungen finden Sie im Referenzpapier [1]. Das Modell besteht aus zwei Spulen und einem Kern. In dem Papier werden 4 Fälle beschrieben. Wir modellieren Fall 2: Die beiden Spulen sind in Reihe geschaltet. Die Reihe wird mit einer sinusförmigen Spannung von 13,5 V (Spitzenwert) gespeist. Zusätzlich liegt eine fünfte Harmonische mit gleicher Phase an.
Geeignete Methode
Jiles Atherton Vector Hysterese Modell
Für die präzise Berechnung der Hysterese in NX Magnetics gibt es eine Implementierung des Jiles-Atherton-Vektor-Hysteresemodells. Hintergrund und die verwendeten Algorithmen sind in [3] und [4] zu finden.
Die Dateien für dieses Beispiel befinden sich im Ordner 'Tutorials/10.Features/10.5MagHysteresisJilesAtherton'. Das Modell ist bereits erstellt und kann im Unterordner complete gelöst werden. Im Folgenden gehen wir durch einige interessante Teile des Modells.
Öffnen Sie in Simcenter die Sim-Datei 'Team32 sim1.sim'. Setzen Sie das angezeigte Teil auf die Fem-Datei.
Überprüfen Sie die vorhandenen Netze und physikalischen Eigenschaften. Beachten Sie auch, dass 1-D-Schaltungselemente enthalten sind, um die Spulen in Reihe zu schalten und zusätzliche Widerstände anzulegen. Zwei verbleibende Spulenanschlüsse sind mit der Spannungslast verbunden, wie später in der Sim-Datei zu sehen ist.
Abbildung: vorhandene Netze, physikalische Eigenschaften und 1-D-Schaltungselemente
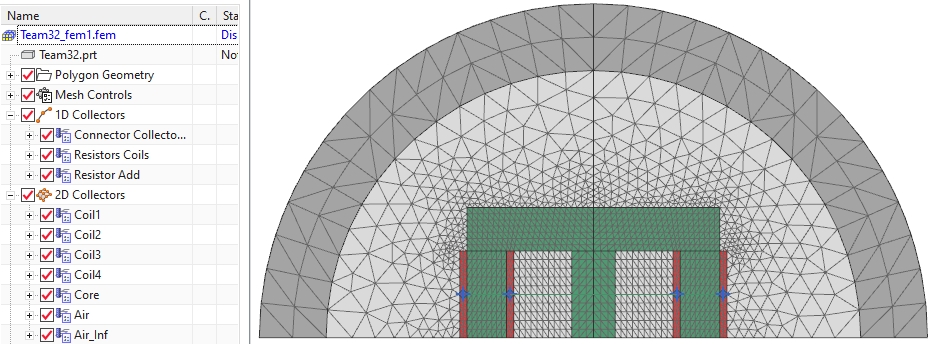
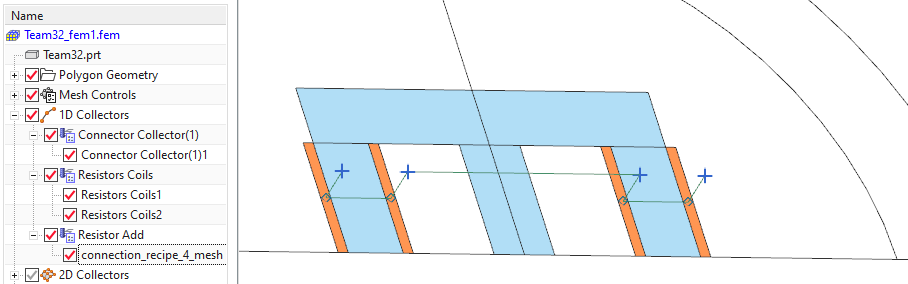
Zur Modellierung der magnetischen Hysterese nach Jiles-Atherton muss die Materialbeschreibung JilesAtherton-Parameter aufweisen. Wir überprüfen dies für das Kernmaterial: Bearbeiten Sie das Kernmaterial (t32 Core mat hyst) und öffnen Sie das Register "Elektromagnetisch".
Bild: Parameter des Materialdialogs mit Jiles Atherton
Prüfen Sie die Last: Beachten Sie, dass es sich um eine Spannungslast handelt, die an den beiden Spulenanschlüssen anliegt. Die Last ist als "analytisch" definiert, da dies die Hinzufügung der fünften Harmonischen ermöglicht, indem man einfach die gewünschte Formel schreibt, wie in der folgenden Abbildung zu sehen.
Abbildung: Sinusspannungslast mit zusätzlicher fünfter Harmonischer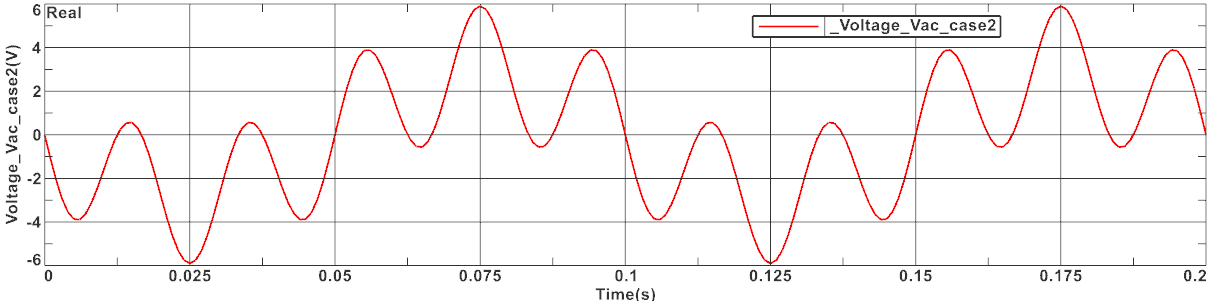
Berechnen Sie schließlich die Lösung. Die Lösungszeit beträgt etwa 3 Minuten für die 200 Zeitschritte und nichtlinearen Iterationen.
Ergebnisse
Simulation - Messung
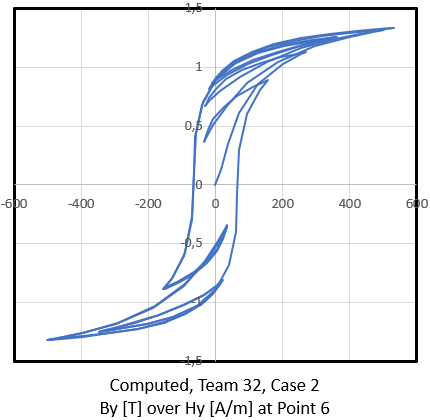
Wir erstellen ein Diagramm b über h und demonstrieren den Hysterese-Effekt. Sie zeigt die gewünschte magnetische Hysteresekurve. Die berechnete Kurve (unten blau) stimmt recht gut mit der Referenzkurve (unten schwarz) überein.
Abbildung: Erwartete (schwarz) und berechnete (blau) Hystereseverlustkurve
Referenzen:
- [1] Description of TEAM Problem: 32. "A Test-Case for Validation of Magnetic Field Analysis with Vector Hysteresis", at the following Link.
- [2] Experimental data to the TEAM 32 benchmark is available at this link.
- [3] "Using a vector Jiles-Atherton hysteresis model for isotropic magnetic materials with the FEM, Newton-Raphson method and relaxation procedure", Guérin C., Jacques K., Sabariego R. V., Dular P., Geuzaine C. and Gyselinck J.
- [4] "Incorporation of a Jiles-Atherton vector hysteresis model in 2D FE magnetic field computations, Application of the Newton-Raphson method", Gyselinck J., Dular P., Sadowski N., Leite J., Bastos J.P.A.



