The electrostatic solution describes the distribution of electric fields due to static charges and / or levels of electric potential. 

Features

• 2D, 3D or axisymmetric Solution, static
• coupled with Thermal solution possible
• Outputs Plot:
  • Electric Fluxdensity, Electric Fieldstrength, Electric Potential (phi-Pot)
• Outputs Table:
  • Capacity, Electrode Voltage, Electrode Charge

Examples

Electrical Feedthrough

Theory and Basics

Formulations

The basis equations:
(1)           rot e = 0
(2)           div d = ρ
(3)           d = ε e

Boundary conditions:
(4)        n x e  | Γ_0e = 0
(5)        n * d  | Γ_0d = 0

Electric scalar potential formulation:
(6)        div ε grad v = - ρ with 
(7)        e = -grad v

Electrostatic weak v-formulation:
(8)        ( -ε grad v, grad v’ )_Ω = 0, 
                for all v’ element of Ω

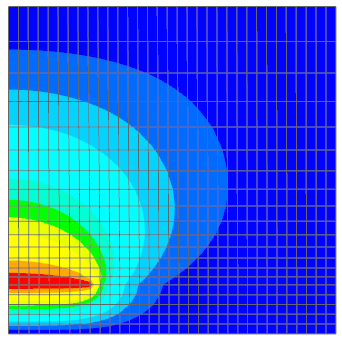
Basic Example: Point and Cylinder

Given is a charge Qf that is applied to a cylindrical face. The face starts at the position (0,0,0) has an radius of R and a length of d. Further there is another charge Q being applied to a point, that is positioned on the axis of the cylinder and has a distance of a (a>d) from the origin. The hole space around has a constant permittivity of ε.

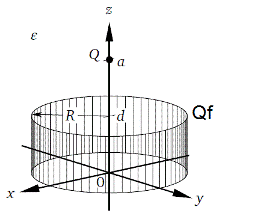
Goal is to analyze for the potential φ along the axis of the cylinder using the following parameters:
Q  =        1e-9 As
Qf=         1e-7 As
a =          0.35 m
d =          0.1 m
R =          0.1 m
ε =          8.85419e-12 F/m

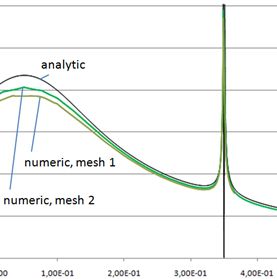
Result: Potential φ

The comparison gives good agreement between theory and numerical solution.