This example shows how a servomotor is analyzed using MAGNETICS and NX NASTRAN. The magnetic forces on 36 teeth are transferred to a structural (acoustic) solve,

Download as PDF     Download NX Files

which gives answers to dominant noise frequency and pressure.

Initial Situation

Stator Vibrations produce Noise

Vibration and noise from in runner electric motors comes mainly from the stator deformation, induced by the constantly varying magnetic field activating individual phases. The deformation on the outer surface of the motor causes the air around it to move, generating pressure differences, which are perceived as noise for the human ear. There are three disciplines to be considered in this analysis—magnetic, vibrational (structural), and acoustic [SantosAnthonisNaclerioGyselinck].

In this use case example we analyze a servo motor for the magnetic and vibrational (structural) disciplines using MAGNETICS for NX and NX NASTRAN. For the third part, acoustics, NX NASTRAN can also be used, but we will not show it here because we focus on the magnetic part.

Goal is to find out which frequencies will appear and which will mainly produce noise while the motor is running at its given speed.

References:

“Multiphysics NVH Modeling: Simulation of a Switched Reluctance Motor for an Electric Vehicle”, Fábio L. M. dos Santos, Jan Anthonis, Francesco Naclerio, Johan J. C. Gyselinck, Member, IEEE, Herman Van der Auweraer, Member, IEEE, and Luiz C. S. Góes. IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, VOL. 61, NO. 1, JANUARY 2014.

Appropriate Method

2D Magnetic, 3D Structural Approach

The results base on magnetic forces on the teeth. For this we will first perform a transient analysis in 2D and compute forces on the teeth. We will use a postprocessing solver feature that converts the time dependent forces into frequency dependent ones using Fourier transformation. Then those frequency forces will be imported into NX10 using the feature load recipe that is new in NX10. Finally in NX a frequency response analysis in NX NASTRAN Solution 111 with those forces as input will be performed.

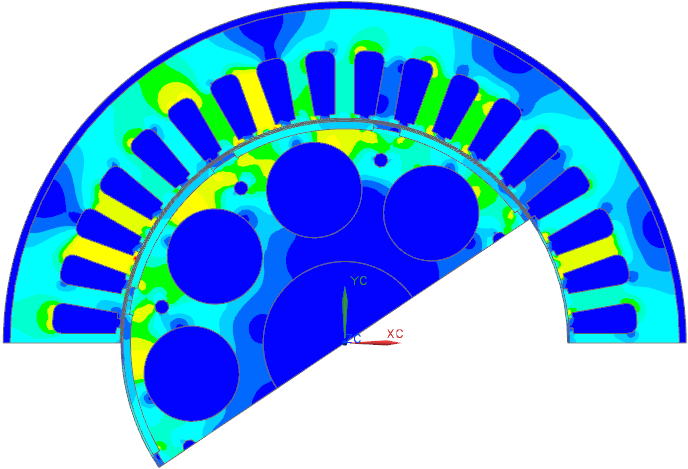Picture: Complete Simulation Model of 1FT6 Motor. Fluxdensity distribution in 1FT6 Servomotor. Two out of four poles are modeled using periodicity conditions. Click to animate

Starting point is an already complete simulation model of a servo motor. We first check it and then add the necessary steps for NVH export and solve in NX NASTRAN. The model must be prepared like shown in the following picture: In the air gap under each tooth there must be a separately meshed face defined.

Picture: Faces in the Air Gap on which Forces are computed

Tangential and radial forces are computed by the following equations based on the Maxwell Stress tensor that is evaluated on the previously defined teeth faces.

The forces should be checked in the first step. They appear like in the upper part of the following picture which shows the forces for the first tooth.

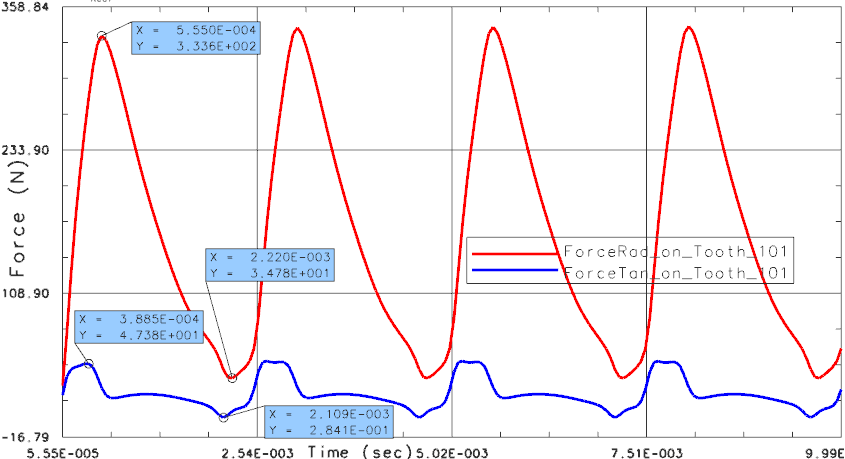
Picture: The Simulation Model computes time domain forces on the 36 teeth in radial and tangential directions

Now the time domain forces are Fourier transformed into frequency domain. So for each tooth we get real and imaginary part as function of the frequency. This is shown in the next picture.

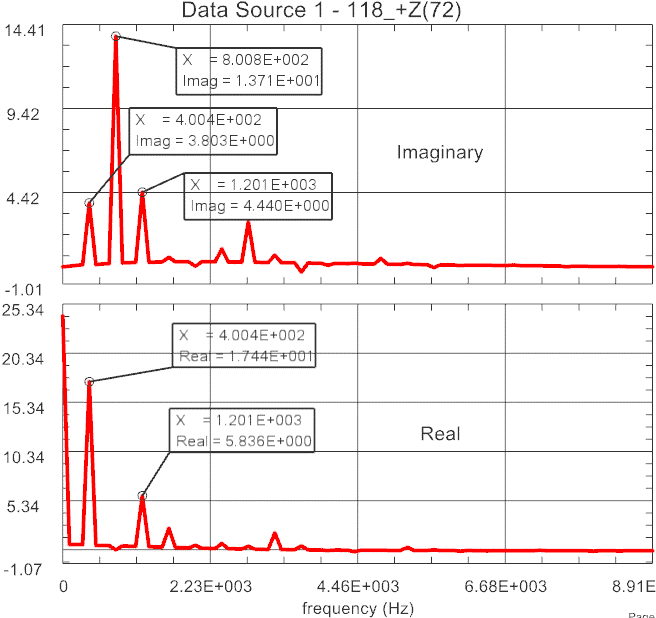
Picture: Fourier transformed Forces

Result

Frequency for highest noise pressure

In the next step a 3D model for structural FE Analysis is set up in NX, which can simply be done by extruding the stator faces. For efficient work this should be done by the assembly fem method which allows meshing only one tooth and reusing it 36 times.

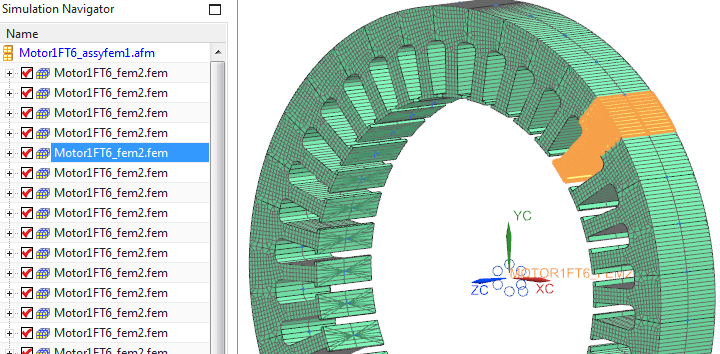Picture: 3D structural assembly mesh in NX for the stator

All previously computed frequency domain forces are applied to the structural mesh now using the NX feature “Load Recipe”. The mapping to the 36 teeth must be done manually only the first time. If there are changes in the magnetic or structural model there is a fully automatic update possible.

The structural FE model can now be used to perform NX NASTRAN dynamic response simulations (Solution 111). For validation of the computed results we show a table with frequencies and the corresponding maximum amplitudes. These information are extracted from the results.

Frequency [Hz]                    max. Amplitude [mm]
100.1                                     0.000131
200.2                                     0.000116
300.3                                     0.000103
400.4                                     0.0029
500.5                                     0.000067
600.6                                     0.000068
700.7                                     0.000072
800.8                                     0.002167
900.9                                     0.000109
1001                                      0.000178
…

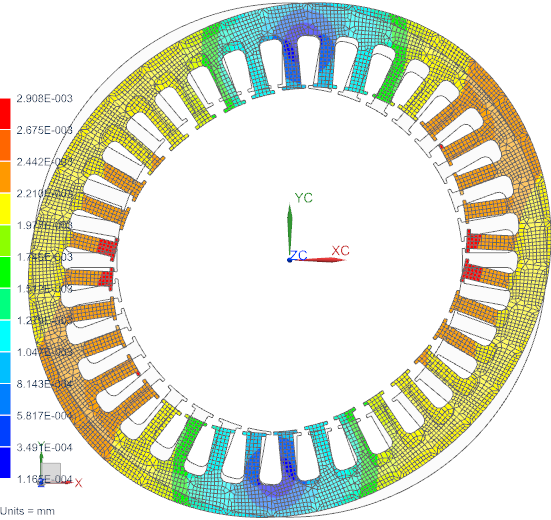
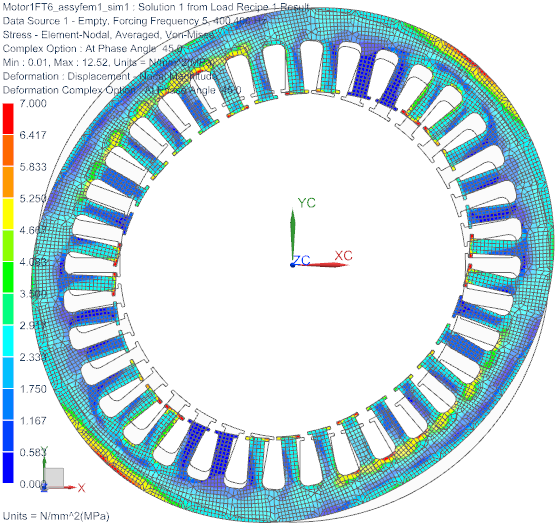
It can be seen that at 400.4 and at 800.8 Hz there are maxima in the amplitude as was requested in the task. This results in the highest noise pressure at this frequency. Finally we show the deformation shape and stress distribution (click to animate) for frequency 400.4 Hz.

Picture: Deformation Shape at critical frequency 400 Hz. Scale is set to 100. Click to animate.

Picture: Von Mises Stress at critical frequency 400 Hz. Click to animate